How to find the taper angle of a (sliced) cone

[stioc]

I have a part (it's a tire balancer cone) of an unknown taper. When I first saw the cone I figured I'd use the right triangle rule but that's not correct because the right triangle's tip isn't the tip of the cone- because the 'cone' doesn't have a point. What's the best way to find its taper angle?

 

[BtoVin83]

Subtract the diameter of the small end from the large end now you have a point at the top

 

[benmychree]

WHAT WOULD BE THE MATTER WITH USING A PROTRACTOR?

 

[stioc]

Subtract the diameter of the small end from the large end now you have a point at the top

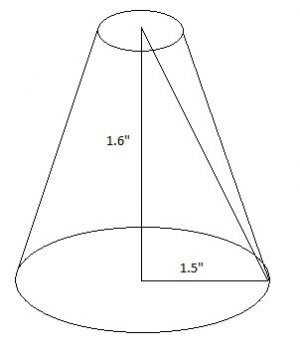
Ah! thanks. So the resulting number will be the large diameter? the height stays unchanged? e.g. say the small end is 1" the large end is 3" so 3-1=2 - I'll use 2 as the bottom diameter.
In other words: X=Inv Tan (Opposite/Adjacent)
X= Inv Tan (1.6/1)
X= 45deg

WHAT WOULD BE THE MATTER WITH USING A PROTRACTOR?

I could just do that but I felt I should use both methods to make sure I'm on the right track. More as an academic exercise than anything else.

 

[petertha]

Not sure I understand your post-4 example, but here is a sketch with resultant dimensions. If your calculator spits out these angles, you are good to go.

 

[Ray C]

You can't solve the problem as shown. You need to specify the small diameter too.

Let D be the big diameter and 'd' be the little diameter then R and r will be their radii respectively. Let H be the height of the cone.

R = D/2
r = d/2

Tan (angle) = (R-r)/H which means: angle = Arctan (R-r)/H

Ray

 

[Ray C]

If you want to know taper, that is normally expressed as inches per foot. The taper of a ramp in the example above would be R-r (in inches) divided by H (in feet). If you want the machine taper, you need to define if you want included angle or not. For included angle it would be D-d (in inches) divided by H (in feet). Check here and you'll see that different standards calculated taper differently (included vs non-included angle). I've encountered this confusion many times. https://en.wikipedia.org/wiki/Machine_taper

As far as the angle calculation in post #6, that is as fundamental as it gets -indisputable.

 

[stioc]

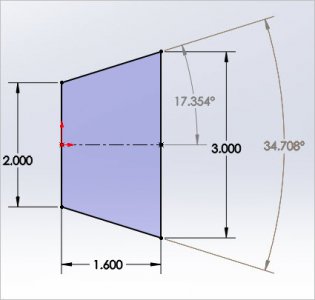
Not sure I understand your post-4 example, but here is a sketch with resultant dimensions. If your calculator spits out these angles, you are good to go.

Thanks Peter. I don't get those angles so I'm trying to figure out the correct math behind it.

You can't solve the problem as shown. You need to specify the small diameter too.

Let D be the big diameter and 'd' be the little diameter then R and r will be their radii respectively. Let H be the height of the cone.

R = D/2
r = d/2

Tan (angle) = (R-r)/H which means: angle = Arctan (R-r)/H

Ray

Thanks Ray- I believe that's exactly how I calculated it but I'm not getting the correct angles. If you want to try it:
D=3
d=2

EDIT: OOPS! you're right! I think in my second post example I didn't use the correct numbers. This is right, YAY! lol
Arctan (1.5-1)/1.6=17.35 deg

Thanks guys!

 

[Ray C]

3/2 = 1.5
2/2 = 1
1.5 - 1 = 0.5/1.6

arctan 0.5/1.6 =17.35 Measured from centerline of cone.




EDITED to show the calculations. I also had to edit this because I can't see a darn thing w/o my glasses using a browser on a mobile phone.

 

[stioc]

Right, I was doing Arctan (H/(R-r) which gave me the angle from the other end but subtracting from 90 would set that straight. Thanks again guys. Now I can't wait to get home and see if the compound slide angle follows the part

 

[MarkM]

Big diameter minus small diameter divided by your taper length. The tangent of this number will give you the angle.

 

[MarkM]

Measure the small diameter. Big diameter minus small diameter divided by taper length. The tangent of this number is your angle.

 

[stioc]

Well that worked guys, the taper's angle based on my measurements came out to be 12.3deg, which was confirmed by the angle gauge/protractor too. My guess is it was 12deg even when it was made. Thanks everyone!

 

[RJSakowski]

Measure the small diameter. Big diameter minus small diameter divided by taper length. The tangent of this number is your angle.

The taper is the difference in diameters divided byr the distance separating them but the half angle (measured between center line and the taper is the arctan of half the taper. The total include angle is twice that angle. Taking the arctan of the taper is close to the total angle but only when the angle is small. For small angle measured in radians, a = tan a = sin a. As the angle increases this equality falls a part. For example , for a 1º angle a = .017453 radians, tan a = .0174655, and sin a = .017452 but for a 45º angle a = .7854 radians, tan a =1, and sin a =.7071. For this reason the equality a = 2 arctan a/2 is not true.

 

[lewey]

i would usually just do as others have said measuring the big and small diameters. if you want to get more precise you can chuck it up and move your carriage across with a dial on your part.

 

[MarkM]

Rj for this example the proper trig function is tangent. Opposite over ajacent. It will give you the included angle. As accurate as can be!

 

[Ray C]

???? See the pictogram from top to bottom. Assuming the dimensions are H =1.6, D = 3 and d = 2 then, the angle wrt horizontal axis is arctan (R-r)/H = 17.35 degrees. The included angle is twice that. The angle at the base end is 90-17.35.




-maybe a CAD image will back me up

 

[stioc]

OP here...per post# 13 above I was able to calculate and verify the correct angle using the ArcTan(R-r/H) forumla.

Ray you're absolutely correct...however, the dimensions I used in this thread were not the actual dimensions of the cone though, hence my results in post #13 were different but the formula was spot on. Thank you and everyone else for that.

 

[RJSakowski]

Rj for this example the proper trig function is tangent. Opposite over ajacent. It will give you the included angle. As accurate as can be!

Mark, There were two errors in your previous post. The first is that to find the angle, you use the arctangent function not the tangent. The second is that you have to use the radii rather than the diameters to determine the angle as stated by Ray in posts 6 & 9. arctan(D/2-d/2)/H = arctan(.5/1.6) =17.354º while (arctan(D-d)/H/2 = 16.00º.

edit: added missing divide by 2

 

[MarkM]

You guys are absolutely right! I am doing my compound setting using taper per foot. Heres what I was thinking. Taper foot is tpf over 24 equals tangent angle. Or not really thinking at all I guess Thanks guys learn something everyday and realize just how much I need to hit the books again. Been away some twenty years after doing for it for twenty. Started in screw machines while doing and app. Program doing general machining. Took a job across country as a general machinist. Not enough work and life. Driven a Zambonii for the last twenty in another town now for work. Lost some people in my life. Realized i miss machining. Seeing something your making evolve. Good for the soul. Sold my two motorcycles and took out the credit card and back into machining at fifty. Still driving a zamboni for now. I Can ramble a bit! But guys I am not too proud and Always willing to learn. Thanks And another realization there is so much and machining is definite. No Horseshoes! Need to sharpen up I guess. Just another great challenge on it s own to learn and be interested!

 

[MarkM]

It s friday guys and gals. Long wkend here on the canadian east coast . Sometimes we wonder what we post. Oh well! been miller time for awhile. Looking forward! Enjoy the wkend!

 

[MarkM]

Holy cow up at 4 am. With my better halfs alarm going off to watch the queen get married. First thing I do is grab my calculater over this trig and my post. I Don t care who is right or wrong. For me its am I That out of touch being out for so long and another question to me if what I am doing with my life crazy. Taking a run at getting my own shop going. Lost all my confidence and second guess myself. Took my old books to verify. Well the trig worked out as I thought after braking it down to a proper triangle? I have a story to tell and been meaning to start a thread about it.
One thing is I Should really think more about what I post especially when i ve had a few. I ll be better and more respectful to all and this forum!

 

[RJSakowski]

Mark, you're not alone. I missed a divide by 2 in my post.

I was up a 5:00AM but not to watch the royal wedding. A week long fishing trip happening tomorrow.