Forgive me if parts of this do not make sense, as I am not sure how to even ask what I want. I wish to learn how to calculate partial circles cut into an object.
Example:

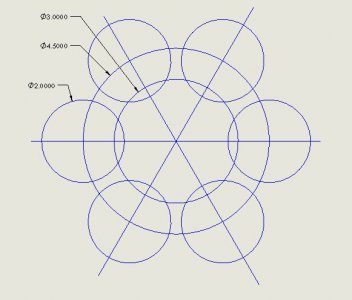
If I have a round knob already, and I want to cut in shallow radii around the circumference, like above, I need to be able to calculate the width of the circle for a given depth of that circle, or once I know the width I want to cut, what diameter cutter will I need to use to get that width while the depth is less than the radius. In the pic, the radii are very shallow, and definitely not half of the diameter of the circle that radius would be part of. Yes, I realize the pictured knob is not cut, but cast in that shape. I am thinking that once I have the circumference measurement of my knob, I then would split it into sections, like above, there would be 6 notches and peaks. I want wanted all of them to be equal width, with a circumference of 3.141 (for a 2" diameter knob), I would divide by 12, which gives me radius and peak width of .2618. Now I need to calculate the width of a circle at, let's say 40% of the radius, so I can figure out what diameter end mill to cut these radii in the knob.
Is any of this making any sense?
I have another practical application for this knowledge as well. I am essentially creating a boring head. I need to cut a notch in one side so the adjustment screw can engage the head to move it. The notch will not be half of the diameter, but maybe a quarter (half the radius), as I need the diameter of the screw to remain in the top part of the head. Learning how to calculate this information will allow me to figure out how much larger I need to make the head of the screw so I can engage the lower part of the head and still have the screw in the top part of the head. See pic below:

Trial and error takes time and materials. I'd rather not waste either if I can learn how to calculate this information.
Thanks,
Chris
Example:

If I have a round knob already, and I want to cut in shallow radii around the circumference, like above, I need to be able to calculate the width of the circle for a given depth of that circle, or once I know the width I want to cut, what diameter cutter will I need to use to get that width while the depth is less than the radius. In the pic, the radii are very shallow, and definitely not half of the diameter of the circle that radius would be part of. Yes, I realize the pictured knob is not cut, but cast in that shape. I am thinking that once I have the circumference measurement of my knob, I then would split it into sections, like above, there would be 6 notches and peaks. I want wanted all of them to be equal width, with a circumference of 3.141 (for a 2" diameter knob), I would divide by 12, which gives me radius and peak width of .2618. Now I need to calculate the width of a circle at, let's say 40% of the radius, so I can figure out what diameter end mill to cut these radii in the knob.
Is any of this making any sense?
I have another practical application for this knowledge as well. I am essentially creating a boring head. I need to cut a notch in one side so the adjustment screw can engage the head to move it. The notch will not be half of the diameter, but maybe a quarter (half the radius), as I need the diameter of the screw to remain in the top part of the head. Learning how to calculate this information will allow me to figure out how much larger I need to make the head of the screw so I can engage the lower part of the head and still have the screw in the top part of the head. See pic below:

Trial and error takes time and materials. I'd rather not waste either if I can learn how to calculate this information.
Thanks,
Chris